B-дерево и его разновидности
B-дерево (читается как «би-дерево», первая латинская буква «B» не означает ничего конкретного) — самобалансирующее дерево поиска, которое проектировалось для эффективного доступа к данным на внешних хранилищах (в 1970 речь идёт о HDD). В отличие от Красно-Чёрного дерева или АВЛ-дерева каждый узел в B-дереве может иметь несколько ключей, которые используются для поиска элемента (здесь и далее иллюстрации приведены из Кормена Т., Алгоритмы. Построение и анализ):
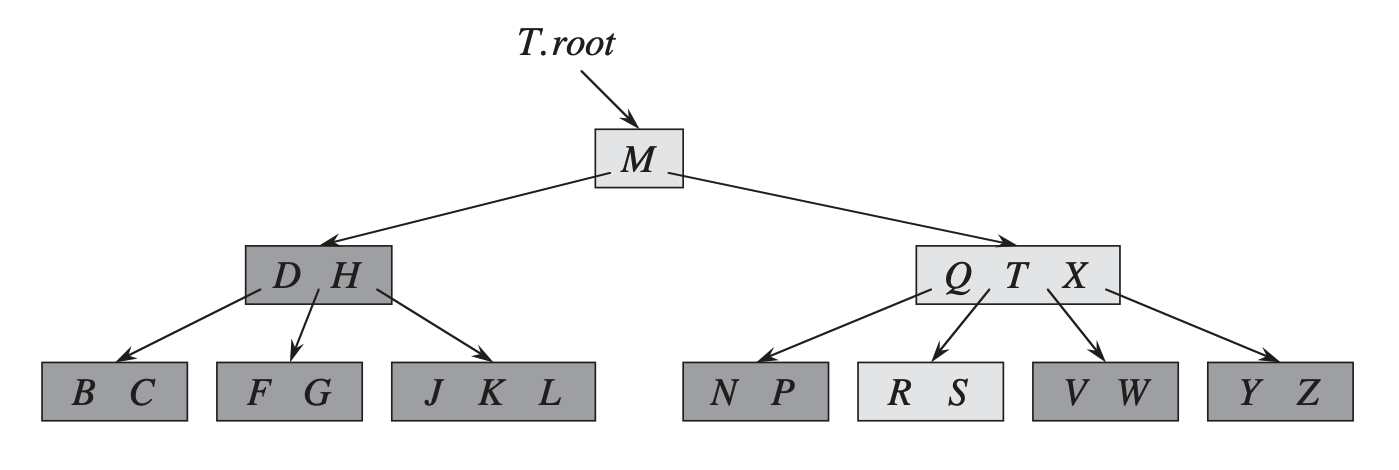
Для B-дерева справедливы следующие ограничения:
- Каждый узел может иметь до
дочерних узлов.
- Каждый нелистовой узел (кроме корневого) имеет как минимум
узлов.
- Корневой узел имеет минимум 2 дочерних узла, за исключением случая, когда он является и листовым.
- Нелистовой узел с
дочерними узлами содержит
ключ.
- Глубина всех листов одинакова.
Для каждого узла дерева справедливы утверждения:
- Ключи узла
—
хранятся в неубывающем порядке:
.
- Каждый внутренний узел также содержит
указателей
на дочерние узлы. Листовые узлы не имеют потомков, поэтому не содержат указателей.
- Ключи
ограничивают диапазон возможных ключей, хранящихся в каждом поддереве: пусть
произвольный ключ в поддереве некоторого узла
, тогда:
- Узел имеет минимальное и максимальное число элементов, которое он может хранить. Определим эти числа через целое число
, называемое степенью B-дерева, тогда:
- Каждый узел кроме корневого должен иметь, по крайней мере,
ключей. Каждый внутренний узел кроме корневого в таком случае хранит по крайней мере
узлов. Если дерево непустое, то узел должен иметь как минимум один ключ.
- Каждый узел может иметь до
ключей. Поэтому, внутренний узел может содержать максимум
узлов. Узлы, содержащие ровно
ключей являются полными
- Каждый узел кроме корневого должен иметь, по крайней мере,
Операции с B-деревом
Поиск элемента
Чтобы найти ключ в дереве достаточно выполнить следующую последовательность действий:
-
1. Загрузить очередной блок (узел) в память с диска.
2. Используя линейный поиск, найти наименьший индекс
3. Если при этом
4. Если узел листовой, то элемент не найден и алгоритм заканчивает работу. В противном случае загрузить блок по адресу
Количество чтений с диска
Поскольку при поиске ключа самой долгой операцией является чтения блоков с диска (где под блоком понимается обычно один узел), необходимо уметь находить количество чтений для элементов. Оно в точности совпадает с высотой дерева, которую для заданной степени
можно рассчитать по формуле:
Добавление ключа
Новый ключ при добавлении всегда помещается в листовой узел, где он должен занять своё место (сохраняя упорядоченность элементов). Но нужный узел может быть уже заполнен, поэтому необходимо уметь разбивать такой узел надвое. Примерный алгоритм выглядит следующим образом (при этом явно запретим дубликаты ключей):
- Осуществить поиск ключа в дереве.
- Если ключ не найден и текущий узел листовой, то добавить ключ на позицию таким образом, чтобы сохранить упорядоченность ключей в узле.
- Если до добавления узел уже являлся полным, то после операции вставки нарушается ограничение на количество ключей в узле, и необходимо выполнить операцию разбиения узла на 2.
Разбиение узла
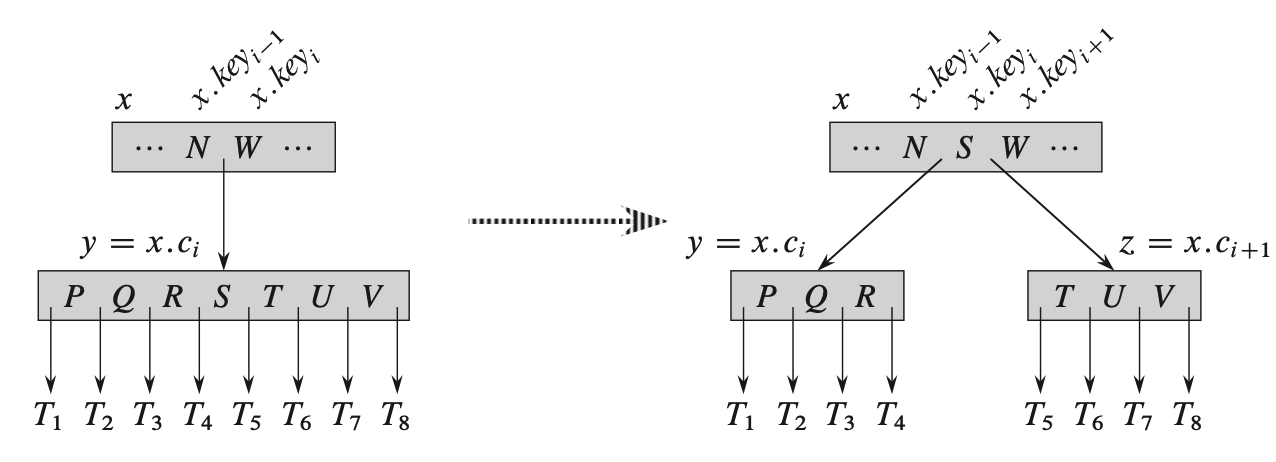
После разбиения в случае, когда родительский узел также оказывается заполненным, то операция разбиения выполняется и для родительского узла. Если таким узлом оказывается корневой, тогда разделение завершается после очередного разделения с созданием нового корневого узла с единственным ключом. Таким образом, B-дерево растёт снизу-вверх.
В качестве упражнение заполните промежуточные операции на приведённой ниже иллюстрации.
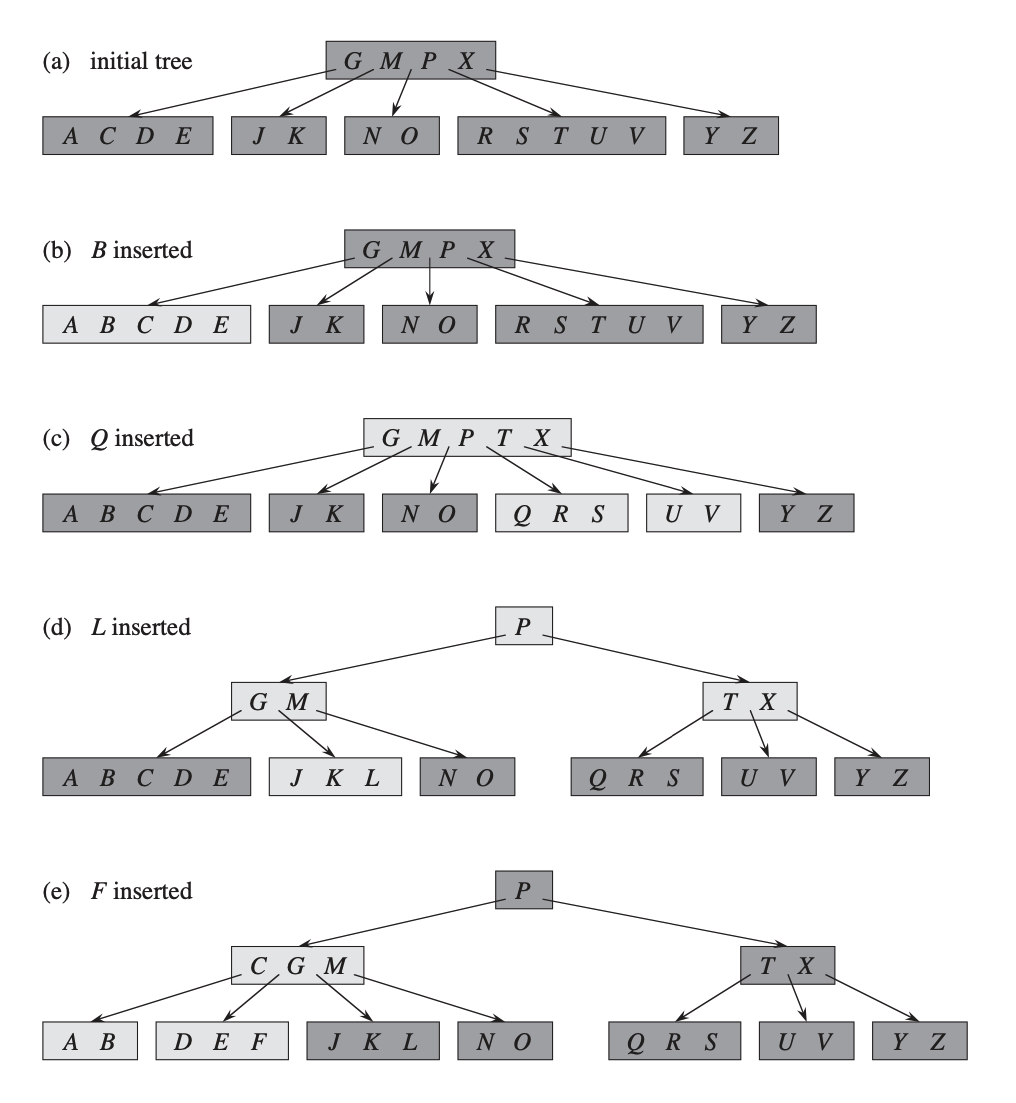
Удаление ключа
Легко понять, что для удаления ключ из дерева достаточно провести процедуру обратную к добавлению. Важно, что при удалении существует возможность удалить ключ из любого узла, а не только листового. Тогда для удаления ключа необходимо для каждого узла, начиная от корневого, проверять следующие шаги:
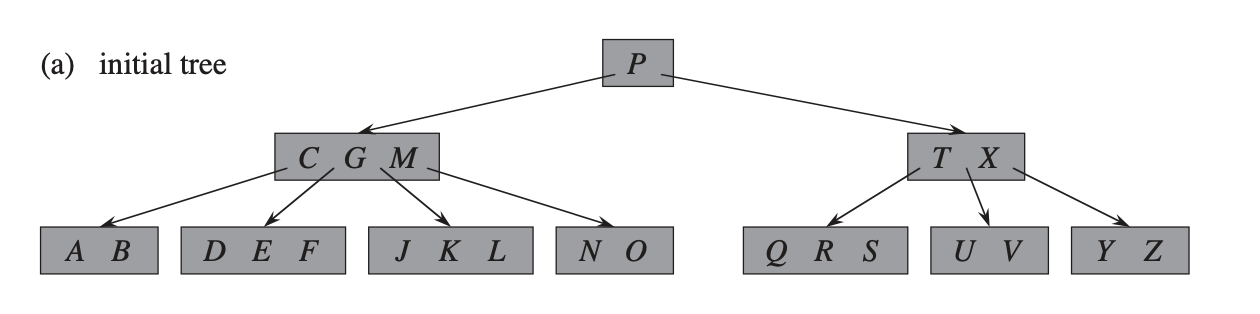
1. Если ключ находится в узле
, являющийся листом, то удалить ключ
из
:
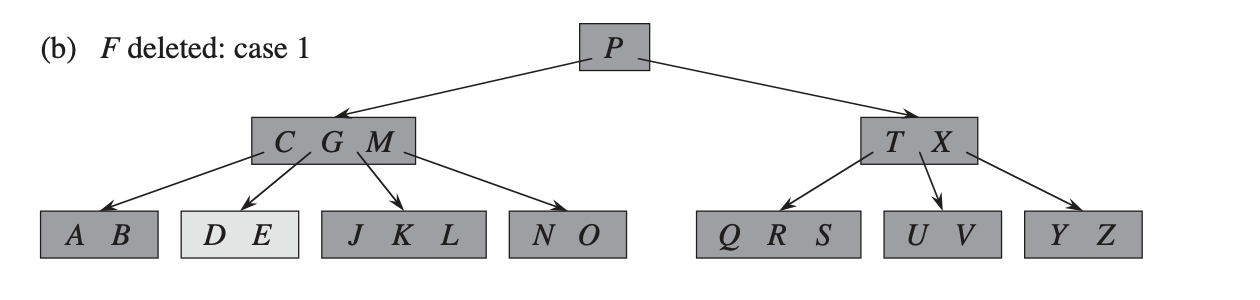
2. Если ключ находится в узле
, являющийся внутренним узлом, то:
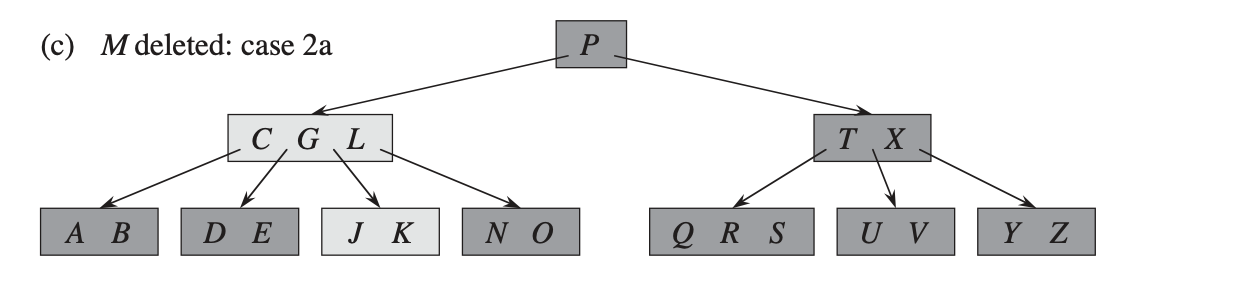
Случай 2a: если дочерний элемент , который предшествует ключу
в узле
, содержит как минимум
ключей, тогда найти в поддереве узла
элемент
, предшествующий
. Рекурсивно удалить
и заменить
на
в узле
.
Случай 2b: если в меньше
ключей, то проверить дочерний элемент
, который следует за
в узле
. Выполнить аналогичную случаю 2a проверку ключа, который идёт следующий по порядку после ключа
.
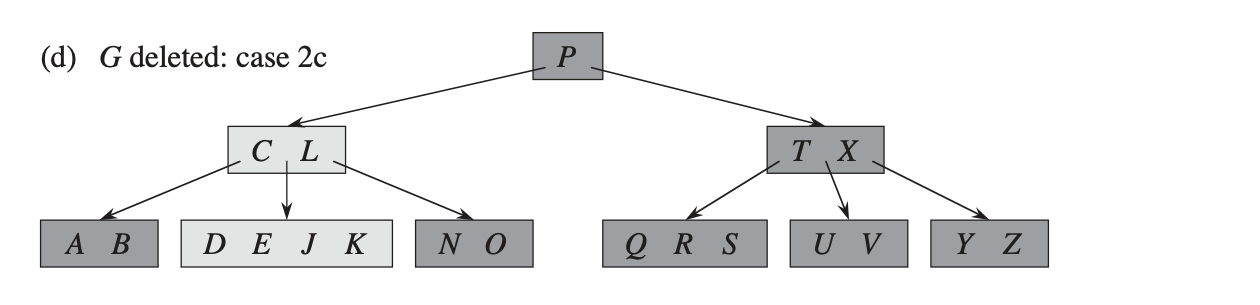
Случай 2c: если оба потомка и
содержат только
ключ, то добавить
и все ключи
в
, после чего из
пропадают
и ссылка на
, а
содержит теперь ровно
ключей. После чего освободить
и рекурсивно удалить
из
.
3. Если ключа нет во внутреннем узле
, то находим поддерево
, которое должно содержать ключ
(если оно вообще есть в дереве). Если
содержит только
ключей, то выполнить 3a или 3b как необходимые шаги, чтобы гарантировать, что мы переходим к узлу, содержащему как минимум
ключей. Затем рекурсивно вызвать удаление ключа
из соответствующего дочернего узла.
Случай 3a: если содержит только
ключ, но при этом имеет непосредственного соседа с не менее чем
ключами, то добавить в
дополнительный ключ путём переноса ключа из
вниз в
, а из соседского узла (справа или слева) перенести ключ в
и обновить ссылку.


Случай 3b: если и оба непосредственных соседа
содержат
ключ, то объединить
с одним из соседних узлов, что влечёт перемещение ключа из
вниз в новый объединённый узел и делает его медианным ключом для этого узла.
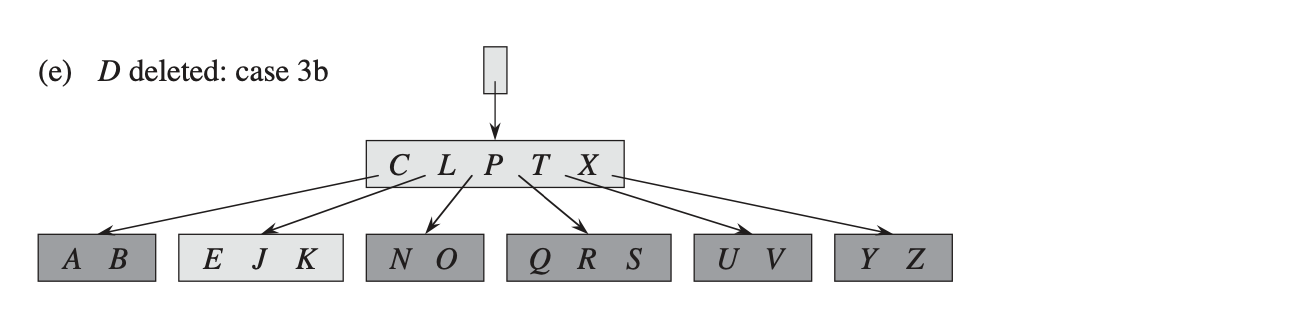

Случай 3b необходим, чтобы при рекурсивном обходе B-дерева от корня к искомому элементу, на каждом у нас была возможность забрать элемент из родительского узла для слияния.