Сравнение алгоритмов поиска подстроки

Существуют несколько классических описанных в разных книгах и статьях алгоритмов, задача которых — это поиск некоторой строки в тексте (ещё говорят поиск подстроки в строке или же образца в строке). Я написал на Джава 17 реализации 4 разных алгоритмов, о которых рассказываю на лекциях, и посмотрел, как они работают на макбуке с процессором М1. Сразу скажу, что эти реализации не являются эталонными и наверняка их можно улучшить. Так, Бойер-Мур достаточно легко ускоряется за счёт замены самописаного OpenTable на что-то вроде Int2IntOpenHashMap Но, тем не менее, почему бы не посравнивать хоть что-то?

Итак, перед тем, как представить 4 алгоритма, участвующих в сравнении, и для всех них будет использоваться этот интерфейс:

public interface StringSearch {

    int find(String pattern, String string);

    default boolean equals(String pattern, String text, int from, int to) {
        for (int i = from; i < to; i++) {
            if (pattern.charAt(i - from) != text.charAt(i)) {
                return false;
            }
        }
        return true;
    }

}

А сами алгоритмы реализуем так:

public class NaiveSearch implements StringSearch {

    @Override
    public int find(String p, String s) {
        for (int i = 0; i <= s.length() - p.length(); i++) {
            if (equals(p, s, i, i + p.length())) {
                return i;
            }
        }
        return -1;
    }
}

public class RabinKarpSearch implements StringSearch {

    @Override
    public int find(String pattern, String string) {
        int patternLength = pattern.length();
        int hs = stringHashCode(pattern, 0, patternLength);
        int stringLength = string.length();
        int st = stringHashCode(string, 0, patternLength);
        for (int i = 0; i <= stringLength - patternLength; i++) {
            if (hs == st && equals(pattern, string, i, i + patternLength)) {
                return i;
            }
            st = st - string.charAt(i) + string.charAt(i + patternLength);
        }
        return -1;
    }

    private int stringHashCode(String string, int start, int end) {
        int result = 0;
        for (int i = start; i < end; i++) {
            result += string.charAt(i);
        }
        return result;
    }
}

public class BoyerMooreSearch implements StringSearch {

    @Override
    public int find(String p, String s) {
        OpenTable table = new OpenTable<>(p.length());
        for (int i = 0; i < p.length() - 1; i++) {
            table.put(p.charAt(i), i);
        }
        loop: for (int i = 0; i < s.length() - p.length() + 1;) {
            for (int j = p.length() - 1; j > -1; j--) {
                if (p.charAt(j) != s.charAt(i + j)) {
                    Integer move = table.get(s.charAt(i + j));
                    i += Math.max(1, j - (move == null ? p.length() : move));
                    continue loop;
                }
            }
            return i;
        }
        return -1;
    }
}

public class KnuthMorrisPrattSearch implements StringSearch {

    @Override
    public int find(String p, String s) {
        var pi = computePrefixFunction(p);
        var q = 0;
        for (int i = 0; i < s.length(); i++) {
            while (q > 0 && p.charAt(q) != s.charAt(i)) {
                q = pi[q];
            }
            if (p.charAt(q) == s.charAt(i)) {
                q = q + 1;
            }
            if (q == p.length()) {
                return i - p.length() + 1;
            }
        }

        return -1;
    }

    private int[] computePrefixFunction(String p) {
        int[] pi = new int[p.length() + 1];
        int k = 0;
        for (int q = 1; q < p.length(); q++) {
            while (k > 0 && p.charAt(k) != p.charAt(q)) {
                k = pi[k];
            }
            if (p.charAt(k) == p.charAt(q)) {
                k = k + 1;
            }
            pi[q + 1] = k;
        }
        return pi;
    }
}

Сам тест, который можно позапускать, лежит в проекте на Гитхабе.

Для тестирования я взял 4 разных текста:

  1. Классический текст Lorem ipsum (445 символов)
  2. Текст «Алисы в стране чудес» (152 173 символов)
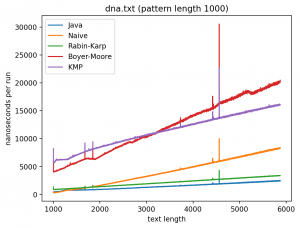
  3. Последовательность ДНК (5872 символов)
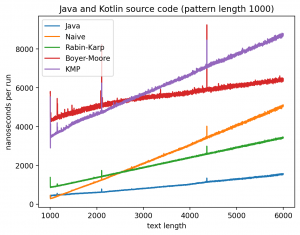
  4. Весь код из одного моего проекта (227 055 символов)

План эксперимента

Каждый текст я прогоню несколько раз и замерю время работы поиска в наносекундах. Подстрока генерируется случайным образом из строки текста. Длина подстроки и текста определяются в зависимости от эксперимента.

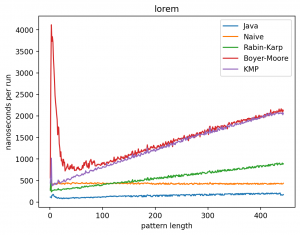
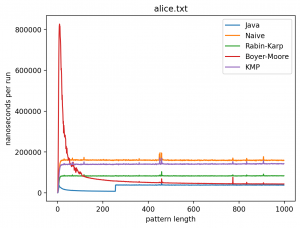
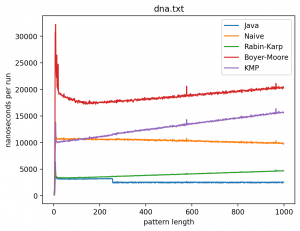
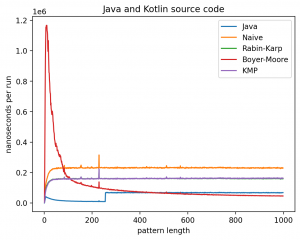
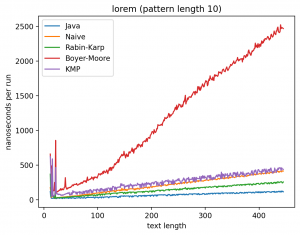
Эксперимент 1: Влияние длины подстроки на время работы

В этом эксперименте длина строки не меняется, а длина подстроки изменяется от 1 до 1 000 (в случае с текстом Lorem до 445). Теоретически, поскольку каждый алгоритм работает за линейное время (кроме наивной реализации) влияние n будет тем больше, чем ближе длина подстроки к длине самой строки. Запуск на MacBook Air M1 2020 дал следующие результаты:

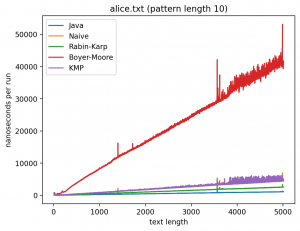
Эксперимент 2: Влияние длины текста на время работы

Теперь будет менять длину текста. От 0 + длина образца до 5000 + длина образца (кроме Lorem), тогда как длина подстроки будет зафиксирована на значения 10, 256 и 1000.

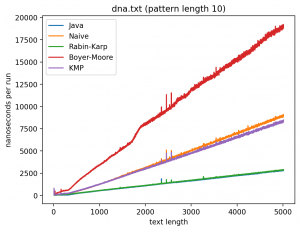
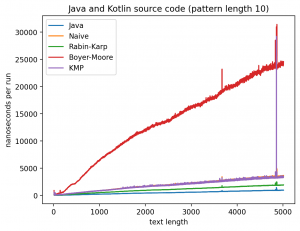
Длина подстроки 10, текста от 10 до 5010:

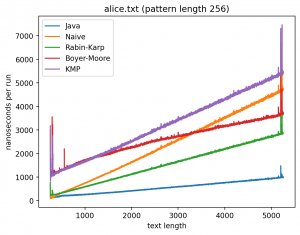
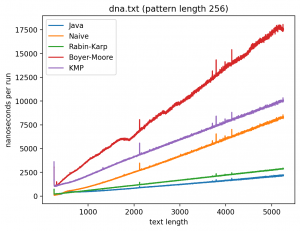
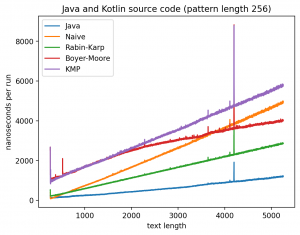
Длина подстроки 256, текста от 256 до 5256:

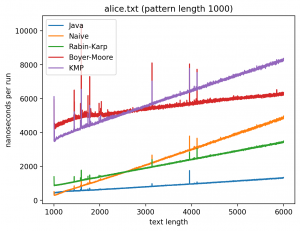
Длина подстроки 1000, текста от 1000 до 6000:

Интересно то, что во всех случаях лучше всего работает самые простые алгоритмы: наивный и его улучшение в виде Рабина-Карпа. Причём последний работает лучше всего. Ещё лучше работает базовая реализация в самой Джаве (String::indexOf). Хотя и тут не без интересного: в эксперименте 1 можно увидеть, как на нескольких графиках время работы резко меняется тогда, когда длина паттерна становится равной 256. О причинах такого я могу догадываться, но попробую изучить вопрос внимательней и прийти с ответом в следующий раз.

Что касается эксперимента 2, то на коротких паттернах хуже всего работает алгоритм Бойера-Мура, но достаточно быстро он начинает реабилитироваться на паттернах в 256 и 1000 символах, за исключением текста с последовательностью ДНК. Это в общем-то согласуется с утверждением о том, что алгоритм Бойера-Мура не так эффективен на текстах с небольшим алфавитом.

Ссылки по теме

  1. Перформанс: что в имени тебе моём?
  2. Exact string matching algorithms
  3. Applied Comparison of String Matching Algorithms
  4. Exact string matching algorithms: Boyer-Moore and KMP
  5. java.lang.String Catechism

Худший вопрос в тесте — это построенный по типу: «Это может быть» с выбором неправильного варианта

Тест всегда должен предлагать выбор только правильных вариантов, а вопрос может быть переформулирован как «Это не может быть».

Короче, вот так вот не надо:

Эти небесные тела являются планетами

Выберите неверные ответы

  • Солнце
  • Земля

А надо так:

Эти небесные тела планетами не являются

  • Солнце
  • Земля

Задачи на JPoint 2018. Luxoft. День 2

Задача 1

public class Quiz_1 {

    public static void print() {
        System.out.print("A");
    }
    
    public static void main(String[] args) {
        ((Quiz_1) null).print();
        System.out.print("B");
    }
    
}

Варианты ответов:

  1. AB
  2. B
  3. NullPointerException
  4. Compilation error
Правильный ответ

1. AB

Из документации 15.12.4.1. Compute Target Reference (If Necessary) instanceof можно узнать, что вызов статического метода не требует вычисления ссылки на инстанс, поэтому никакой ошибки не произойдёт.

Задача 2

public class Quiz_2 {

    public void func(Integer i) {
        System.out.println("integer"); }
    public void func(Double i) {
        System.out.println("double"); }
    public void func(Object i) {
        System.out.println("object"); }

    public static void main(String[] args) {
        List nums = Arrays.asList(1/2);
        new Quiz_2().func(nums.get(0));
    }
}

Варианты ответов:

  1. integer
  2. double
  3. object
  4. Runtime exception
  5. Compilation error
Правильный ответ

3. object

… из-за того, что список List<?> nums типизирован <?>. Такой вайлдкард вернёт Object в любой ситуации, а компилятор заранее скомпилирует представленный код с вызовом правильной функции, а именно public void func(Object i) {.

Задача 3

public class Quiz_3 {

    public static void main(String[] args) {
        System.out.println(
                true?false:true == true?false:true
        );
    }
}

Варианты ответов:

  1. true
  2. false
  3. Compilation error
Правильный ответ

2. false

Тернарный оператор вычисляется слева направо.

Задача 4

public class Quiz_4 {

    public static void main(String[] args) {
        int n = 1;
        int result = Optional.of(n++)
                .map(i -> i + n)
                .orElse(-1);
        System.out.println(result);
    }
}

Варианты ответов:

  1. 2
  2. 3
  3. 4
  4. -1
  5. Runtime exception
  6. Compilaction error
Правильный ответ

6. Compilation error

Переменная n должна быть финальной, чтобы использоваться в лямбда-выражении i -> i + n. С другой стороны, n не может быть финальной из-за унарного оператора ++ в выражении Optional.of(n++).

Задача 5

public class Quiz_5 {

    public static void main(String[] args) {
        int n = Integer.MAX_VALUE;
        n++;
        System.out.println(n + n);
    }
}

Варианты ответов:

  1. -2
  2. 0
  3. 2
  4. 4294967296 (2^32)
  5. Runtime exception
  6. Compilation error
Правильный ответ

2. 0

Начнём с того, что Integer.MAX_VALUE + 1 = Integer.MIN_VALUE. В бинарном представлении значение Integer.MAX_VALUE (01111111111111111111111111111111) при добавлении к нему единицы получится Integer.MIN_VALUE (10000000000000000000000000000000). При сложении 2-х этих чисел сумма старших битов даст 102, что приведёт к переполнению в памяти. Поскольку 1 будет некуда записать в 32-х битном представлении, то останутся только нули.