Анализ алгоритмов

Нашли ошибку в тексте? Выделите ошибку в тексте и нажмите Ctrl + Enter на любой странице сайта.

Несмотря на то, что производительность компьютеров постоянно возрастает, она не может быть бесконечно большой. Поэтому, время вычисления — это ограниченный ресурс, так же, как и объём необходимой памяти. В случае, когда речь идёт именно о времени вычисления, мы будем употреблять термин «временная сложность». Если речь будет идти о памяти в каком-либо виде, то будет говорить «пространственная сложность».

Простой способ оценить работу алгоритма — это посчитать количество инструкций, необходимых для его завершения. Это могут быть ассемблерные команды или инструкции трёхадресного кода. Поскольку любой алгоритм должен быть разбит на шаги, то всегда будет возможность эти шаги сосчитать.

При добавлении одного цикла приходится умножать количество инструкций, заключенных в теле цикла, на количество итераций. В этом случае, говорят, что алгоритм линейно зависит от числа итераций n. Часто этот параметр задаётся неявно, как размер входного массива данных. В таком случае говорят о линейной зависимости от размера данных.

fun findMax(list: IntList): Int {
  var max = list.first()
  for (i in 0 until list.size) {
    if (list[i] > max) {
      max = list[i]
    }
  }
  return max
}

В случае вложенных циклов количество итераций перемножаются. Если количество итераций в циклах равное, то можно говорить про квадратичную зависимость. Такие оценки работы алгоритма часто встречаются при работе с матрицами, изображениями и в других структурах, в которых необходимо обрабатывать строки и столбцы.

fun isIdentityMatrix(list: List): Boolean {
  for (i in 0 until list.size) {
    val row = list[i]
    if (row.length != list.size) {
      return false;
    }
    for (j in 0 until row.size) {
      if (j == i && row[i] != 1) return false;
      if (j != i && row[i] != 0) return false;
    }
  }
  return true
}

Для понимания того, как зависимость от размера данных влияет на общее время работы алгоритма, рассмотрим следующий пример. Допустим, существуют 2 разных алгоритма, решающих одну и ту же задачу. Первый алгоритм решает задачу за $2n^2$ команд, второй алгоритм за $50n log_2⁡n$ . Попробуем сравнить время их выполнения на двух разных компьютерах А и Б. Предположим также, что компьютер А в тысячу раз быстрее компьютера Б и выполняет $10^{10}$ команд в секунду. Запустим первый алгоритм на компьютере А, а второй на компьютере Б для n= $10^7$ .

Более быстрый компьютер с менее эффективным алгоритмом при наших вводных отработает примерно за 5 с половиной часов. Медленный компьютер с более эффективным алгоритмом справится с задачей менее чем за 20 минут.

Как мы можем видеть, зависимость числа инструкций от входных параметров влияет намного сильнее, чем увеличение производительности вычислительной машины.

Рост целевой функции $T(n)$ имеет различные названия:

Константное (время работы не зависит от n)
Логарифмическое ( $\log⁡ n$ : напр., двоичный поиск)
Линейное ( $n$ : напр., поиск максимального значения)
Квазилинейное ( $n \log ⁡n$ : напр., большинство эффективных сортировок)
Квадратичное ( $n^2$ : напр., обход значений матрицы)
Полиномиальное ( $n^c$ для c>1)
Экспоненциальное ( $c^n$ для c>1)
Факториальное ( $n!$ : напр., задача коммивояжёра)

При определённом наборе данных алгоритм может иметь разную временную сложность. Так, к примеру, простая реализация сортировки пузырьком работает за квадратичное время, то есть за $n^2$ для всех входных данных. Но при простой модификации, которая проверяет, что входной массив данных уже отсортирован, достаточно одного прохода по всем элементам. Другими словами, если запустить сортировку для отсортированного массива, что будет являться лучшим случаем, то алгоритм выполнится за линейное время. В таком случае говорят, что алгоритм работает за линейное время в лучшем и за квадратичное время в худшем случае.

Иногда посчитать работу алгоритма в худшем или лучшем случае не представляется возможным. Тогда для оценки скорости роста функции применяют подсчёт в среднем.

Для выполнения подсчёта в среднем используется вероятностный анализ алгоритма. Суть которого заключается в определении всех вероятностей получить на вход какие-то входные значения заданного размера n, после чего рассчитывается математическое ожидание соответствующей случайной величины, как сумма произведения времени работы определённого набора величин на его вероятность.

Обозначим время работы некоторого алгоритма $A$ , на вход которого подаётся вход x, как $C_A(x)$ . Для определения среднего случая рассмотрим конечное множество $X_n=\{x : ||x|| = n\}$ входов размеров n. Предположим, что каждому входу $x \in X_n$ приписана вероятность $P_n(x)$ . На заданном таким образом вероятностном пространстве сложностью в среднем называют математическое ожидание соответствующей случайной величины:

$T_A(n) = \sum_{x \in X_n} C_A(x)P_n(x)$

Например, для алгоритма двоичного (бинарного) поиска среднее время работы можно определить, следуя следующим соображениям: вероятность найти элемент на первом шаге равна $\frac{1}{n}$ , где n — длина отсортированной последовательности. Если на первом шаге элемент не найден, то найти его в подпоследовательности размером n/2 равна $\frac{2}{n}$ , в подподследовательности размером n/4 соответственно $\frac{4}{n}$ . Тогда вероятность обнаружить элемент на i-м шаге будет $\frac{2^{i - 1}}{n}$ . Максимум таких шагов может быть $\log_2 n$ , тогда среднее количество шагов которое нужно сделать для того, чтобы найти элемент будет:

$T(n) = \sum_{x=1}^{\log_2 n} i\frac{2^{i - 1}}{n} = \frac{1}{n}\sum_{x=1}^{\log_2 n} i 2^{i - 1}$

$\sum_{i=1}^{\log_2 n} i 2^{i - 1} = n \log_2 n - n + 1$

Расчёт на Wolfram Alpha

$T(n) = \frac{n \log_2 n - n + 1}{n} \approx \log_2 n$

Асимптотический анализ

Расчёт значений с точными коэффициентами является сложным, а иногда и невозможным. В этом случае удобно абстрагироваться от некоторых деталей. Допустим, что для некоторого алгоритма среднее время работы можно выразить полиномом второй степени. Несомненно было бы удобно упростить его, чтобы:

не учитывать информацию, которая несильно влияет на итоговую формулу,
легко было оценивать время работы,
легко было сравнивать алгоритмы между собой.

Для этого можно использовать вместо точной оценки временной сложности её асимптотическую оценку, которая может быть выражена одной из 3 греческих букв:

Θ(g(n)) — асимптотически точная граница. Тогда для такой функции g(n) это обозначение будет означать множество таких функций, что:

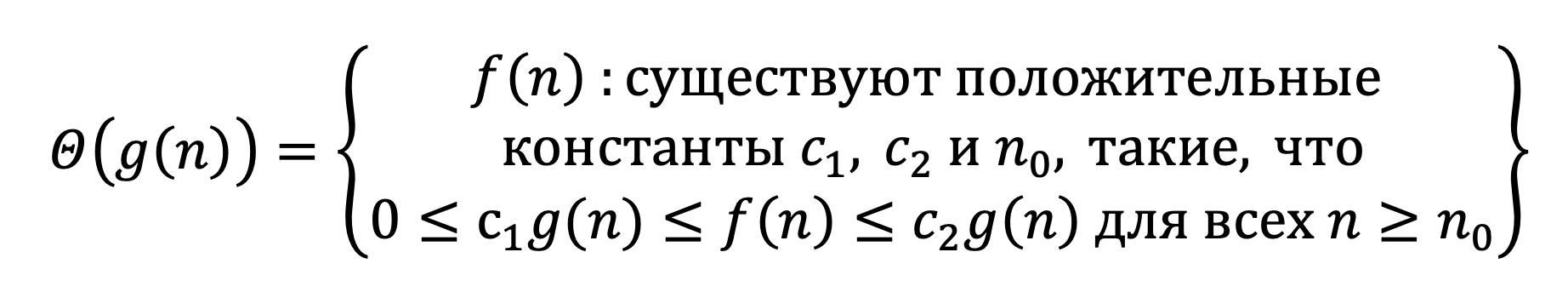
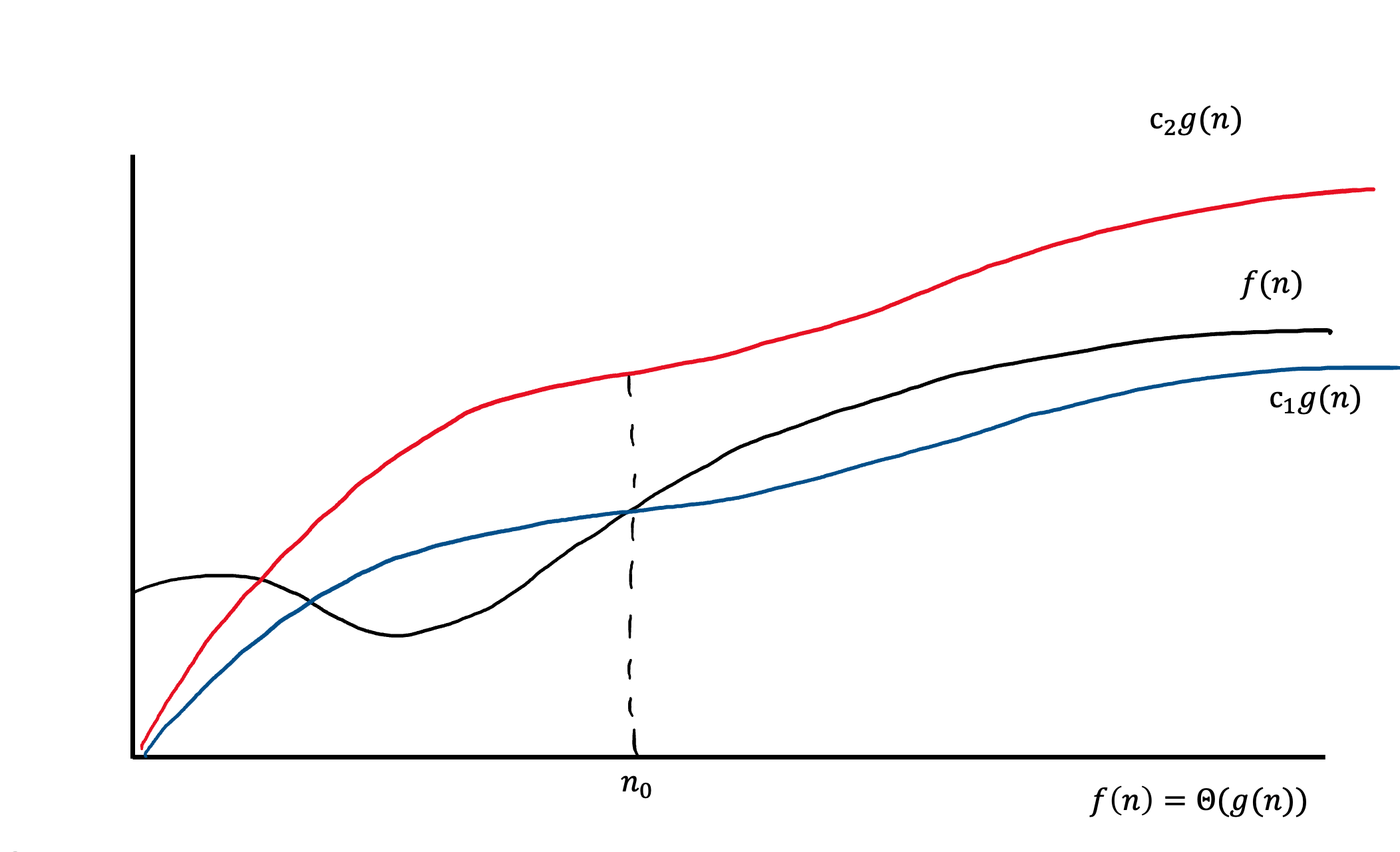
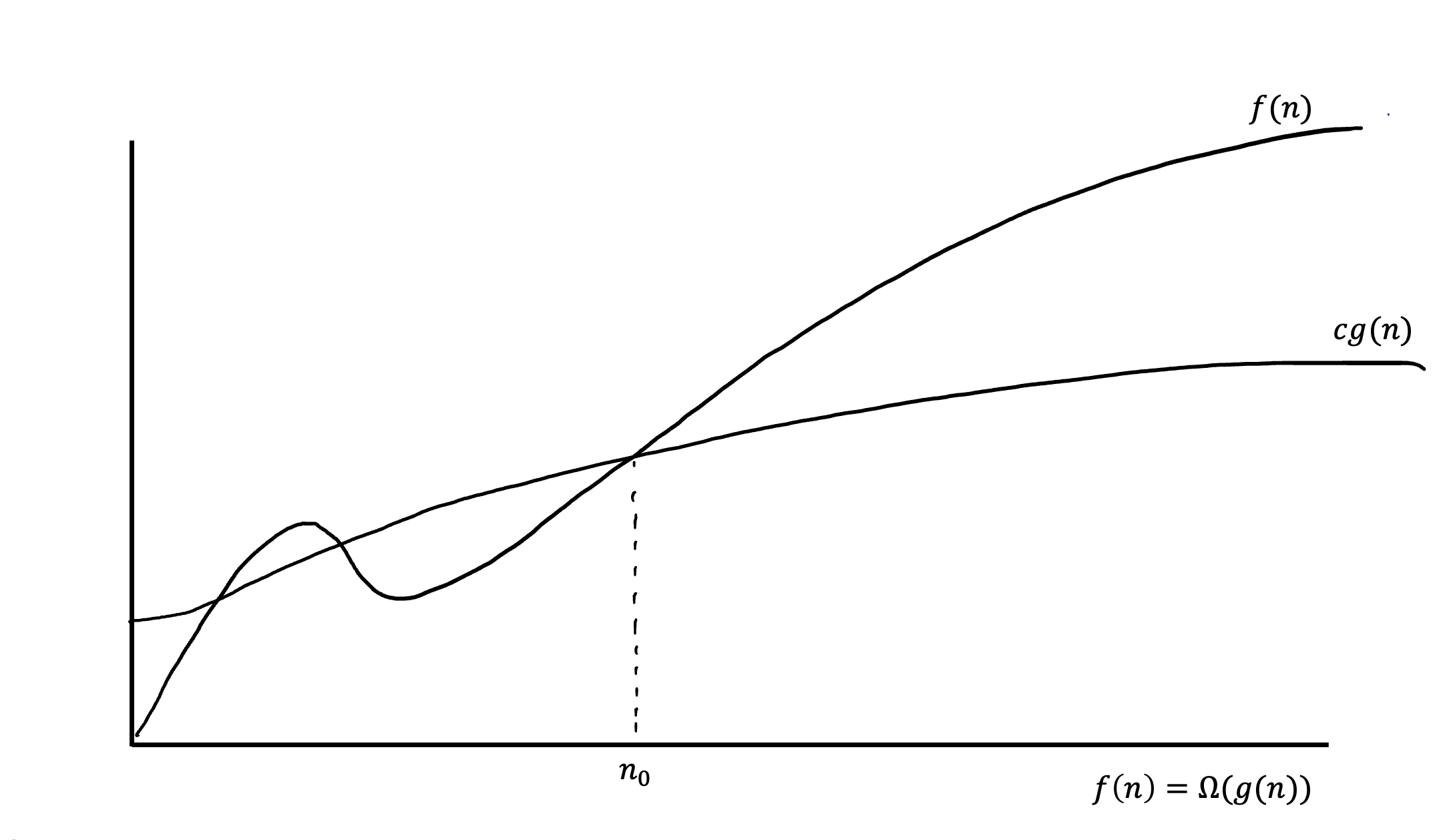
Другими словами, эту оценку можно применять ко всем функциям, которые оказываются стиснутыми между красным и синем графиками. На изображении видно, что эти графики являются одной и той же функцией, взятой с разным коэффициентом. Также, эти функции могут вести себя иначе до некоторого значения $n_0$ .

Ο(g(n)) — асимптотически верхняя граница, для которой все функции будут находиться ниже. Более формально:

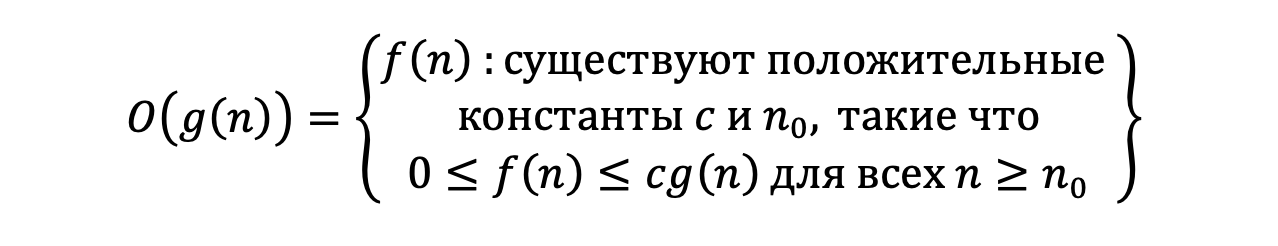
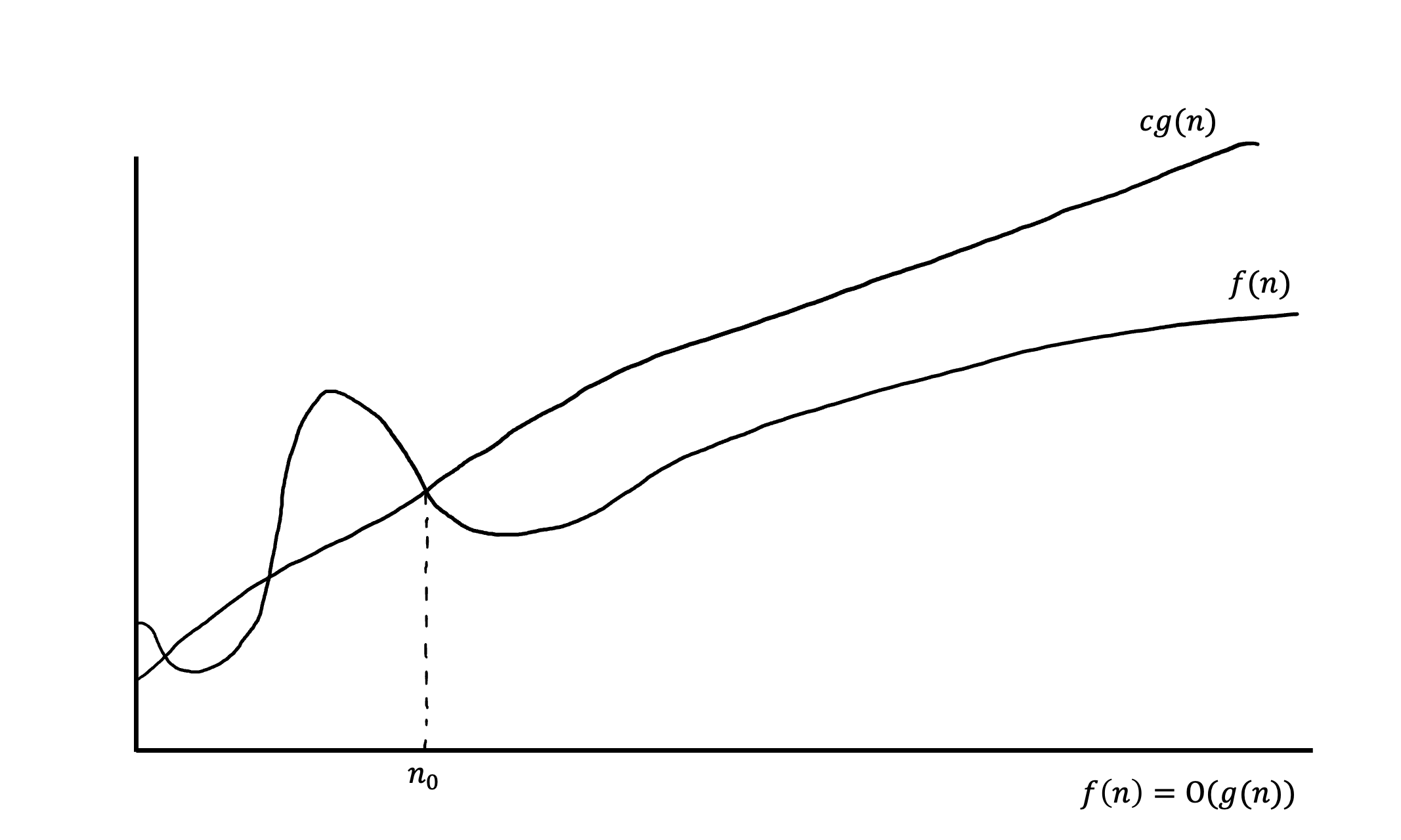
Ω(g(n)) — асимптотически нижняя граница, для которой все функции будут находиться выше. Или опять же более формально:

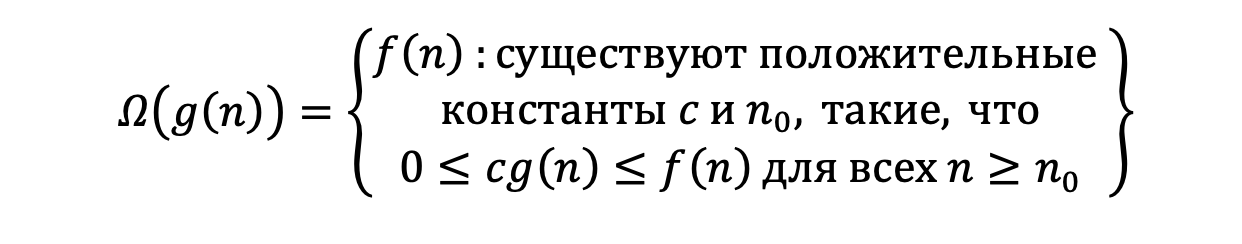
Свойства асимптотических функций

Транзитивность:

Из f(n) = Θ(g(n)) и g(n) = Θ(h(n)) следует f(n) = Θ(h(n))
Из f(n) = Ο(g(n)) и g(n) = Ο(h(n)) следует f(n) = Ο(h(n))
Из f(n) = Ω(g(n)) и g(n) = Ω(h(n)) следует f(n) = Ω(h(n))

Рефлексивность:

f(n) = Θ(f(n))
f(n) = Ο(f(n))
f(n) = Ω(f(n))

Симметрия:

f(n) = Θ(g(n)) тогда и только тогда, когда g(n) = Θ(f(n))

Перестановочная симметрия:

f(n) = Ο(g(n)) тогда и только тогда, когда g(n) = Ω(f(n))

Оценка работы рекурсивных алгоритмов

Рекурсивными являют такие алгоритмы, которые в ходе работы могут вызывать сами себя с другими аргументами. Обычно, размер данных для обработки при этом уменьшается. Это свойство лежит в основе концепции «Разделяй и властвуй». Для них в алгоритме можно выделить 3 основных шага:

Разделение задачи на несколько подзадач, которые представляют собой меньшие экземпляры той же задачи.
Обработка подзадач путём их рекурсивного решения. Если размеры подзадач малы, то такие подзадачи решаются непосредственно.
Комбинирование подзадач в решение исходной задачи.

Возьмём для примера работу двоичного поиска. Здесь время работы будет константным, если n = 1, либо суммой времени работы подзадачи и собственными задачами. В задаче двоичного поиска к собственным задачам относятся, например, получение элемента по нужному индексу, сравнение его с искомым элементом, определение, какую из двух половин выбрать для дальнейшего поиска. Подзадача же на каждом шаге уменьшается вдвое. Всё это можно выразить в виде рекуррентного соотношения.

$T(n) = \begin{cases} \Theta(1), \text{when } n = 1 \\ T(\frac{n}{2}), \text{when } n > 1 \end{cases}$

Существуют разные методы для определения общего времени работы рекурсивных алгоритмов, например:

Метод подстановки
Дерево рекурсии
Мастер-теорема

Метод подстановки

Суть метода подстановки заключается в попытке «догадаться», как будет выглядеть оценка функции, после чего методом индукции проверить её на правильность.

Покажем это для двоичного поиска, для которого известно, что $T(n)=T(\frac{n}{2})+Θ(1)$ .
Сначала докажем, что в индукции срабатывает переход от предыдущего значения к следующему. Допустим, что $T(n) = O(\log_2 ⁡n)$ . Тогда необходимо показать, что $T(n) \le c \log_2 ⁡n$ для правильно подобранного значения $c>0$ .

Предположим, что это ограничение уже верно для всех значений $m<n$ . Например, для $m=\frac{n}{2}$ , тогда $T(\frac{n}{2}) \le c \log_2⁡ \frac{n}{2}$ . Подставляя в исходное рекуррентное соотношение получаем:

$T(n) = T(\frac{n}{2}) + \Theta(1) \le c \log_2⁡ \frac{n}{2} + d = c \log_2⁡ n - c + d \le c \log_2⁡ n$

Последнее неравенство выполняется при c ≥ 1 и d ≤ c. А значит шаг индукции доказан.

Теперь необходимо найти базис индукции. Поскольку $T(1) = d$ , а $c \log_2⁡ 1 = 0$ для любого c, выражение $T(1) \le c \log_2⁡ 1$ не является истиной и не может быть базой, если d > 0. Воспользуемся тем, что для асимптотических оценок достаточно найти $n_0$ при котором соотношение становится верным:

$T(1) = d, c \log_2 ⁡1 = 0 \Rightarrow d \le 0$

$T(2) = 2d, c \log_2 ⁡2 = c \Rightarrow 2d \le c$

$T(4) = 3d, c \log_2 ⁡4 = 2c \Rightarrow 3d \le 2c$

Возьмем базис при $n_0 = 2$ , тогда при $c = 2d$ индукция будет доказана.

Метод дерева рекурсий

В методе дерева рекурсии все вызовы изображаются в виде дерева, для каждого вызова определяется его стоимость, после чего достаточно будет посчитать сумму всех стоимостей.

Рассмотрим дерево рекурсии для двоичного поиска. В нём каждый узел, начиная с корневого, будет порождать только одну ветвь работы алгоритма: алгоритм выбирает либо левую, либо правую половину. Всего таких разбиений будет $\log_2 ⁡n$ , т. к. при каждом разбиении размер входных данных уменьшается вдвое. Показать, это можно, определив, что на k-ом вызове функции размер входных данных уменьшится ровно в $\frac{n}{2^k}$ . Если зафиксировать, что на этом шаге размер данных равен 1, то решив уравнение получается, что $n = 2^k \Rightarrow k = \log_2 ⁡n$ , где k — последний шаг рекурсии и высота дерева.

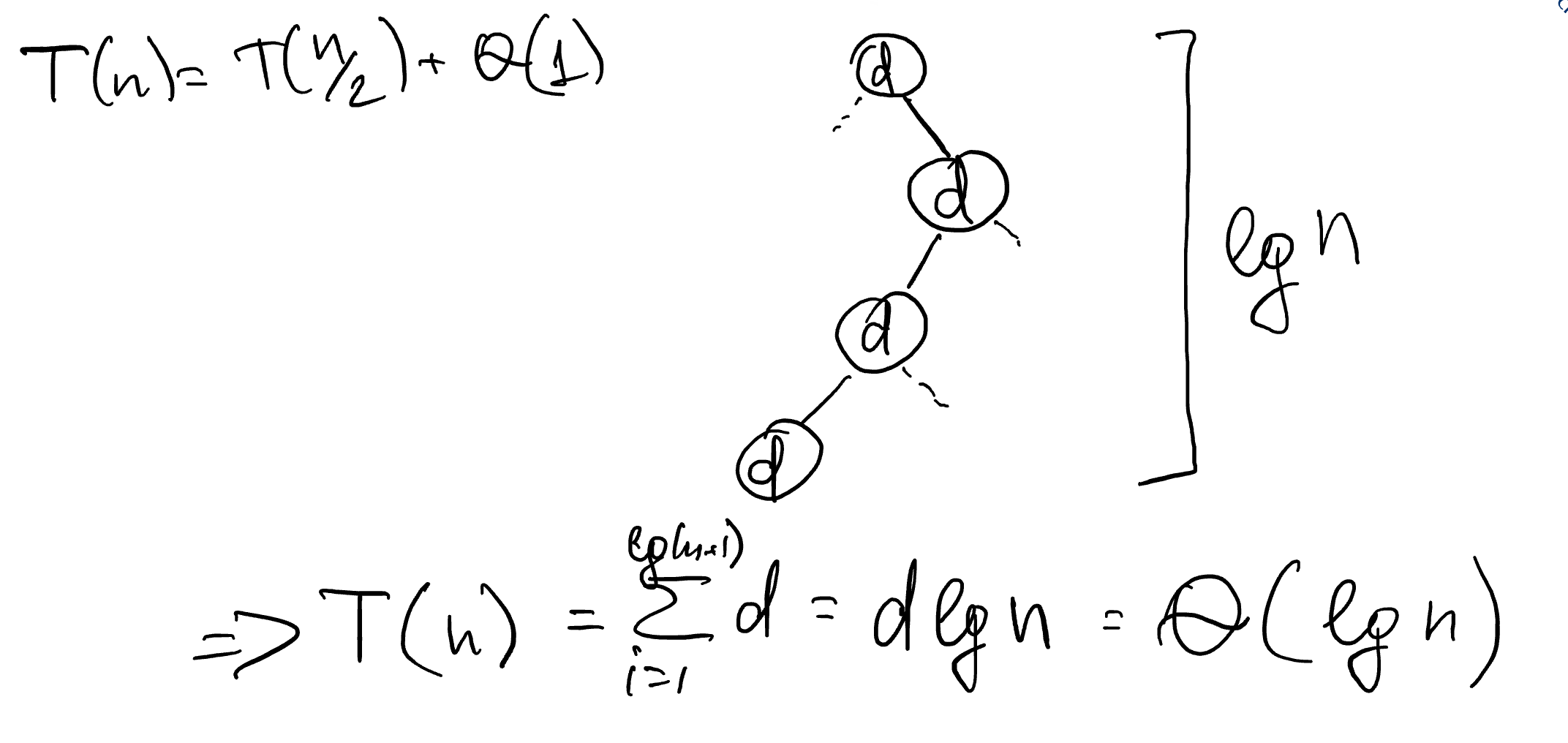
Просуммировав стоимость каждой операции d k раз определим, что:

$T(n) = d \log_2 ⁡n = \Theta(\log_2 ⁡n)$

Рассмотрим другой пример, где стоимость каждого узла линейно зависит от размера данных, а каждая задача разбивается на 4 подзадачи, в каждую из которых уходит половина данных. Тогда на i-м уровне получаем стоимость обработки подзадачи как $4^i \frac{cn}{2^i}$ .

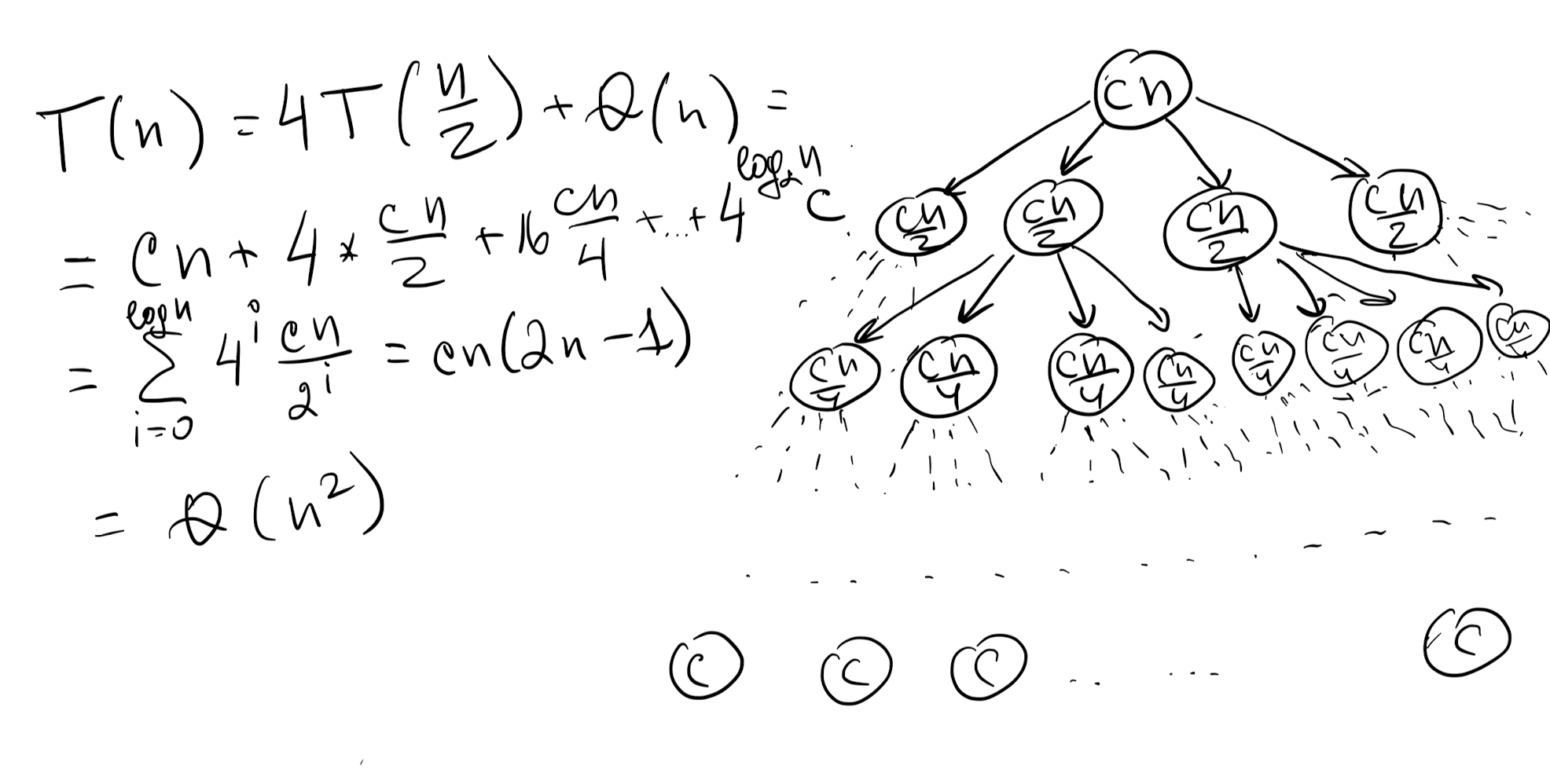
Высота дерева напрямую зависит от того, как быстро уменьшается количество данных. В данном случае на каждом уровне количество данных в 2 раза меньше, а следовательно высота дерева будет ограничена $\log_2 n$ . Тогда просуммировав все элементы получим, что:

$T(n) = cn(2n - 1) = \Theta(n^2)$

Мы рассмотрели простые случаи, но в реальности деревья могут делиться не на равные части, например, рекуррентное соотношение может выглядеть так:

$T(n) = 3T(\frac{n}{5}) + 2T(\frac{n}{4}) + T(\frac{n}{3})$

Мастер теорема

Самым простым методом определения времени работы считается использование мастер-теоремы. Суть которого в том, что рекуррентное соотношение можно представить в общем виде как:

$T(n)=aT(\frac{n}{b})+f(n)$

где a ≥ 1, b > 1, а f(n) — заданная функция. Здесь a означает количество подзадач, на которое делится исходная подзадача, а b — во сколько раз уменьшается количество данных при вызове рекурсивной функции. f(n) — это работа по обработке 1 вызова метода рекурсии. Далее ответ зависит от одного из трёх случаев, с помощью которого асимптотические оценки определяются достаточно просто:

Если $f(n) = O(n^{\log_b⁡ a - \epsilon})$ для некоторого ϵ > 0, то $T(n) = \Theta(n^{\log_b⁡ a})$
Если $f(n) = \Theta(n^{\log_b ⁡a})$ , то $T(n) = \Theta(n^{\log_b a} \log_2 ⁡n)$
Если $f(n) = \Omega(n^{log_b⁡ a + \epsilon)$ для некоторого ϵ > 0 и если $a f(\frac{n}{b}) \le c f(n)$ для некоторой c < 1, то $T(n) = \Theta(f(n))$

Рассмотрим её применения для двоичного поиска:

$T(n) = T(\frac{n}{2}) + d$

Поскольку $d = \Theta(n^{\log_2⁡ 1}) = \Theta(n^0) = \Theta(1)$ , то срабатывает второе правило мастер-теоремы и ответом является:

$T(n) = \Theta(n^{\log_2 ⁡1} log_2 ⁡n) = \Theta(\log_2 ⁡n)$

Рассмотрим другой пример рассмотренный раннее. Пусть:

$T(n) = 4T(\frac{n}{2}) + kn$

Попробуем применить 3-е правило мастер теоремы, где a = 4, b = 2 и проверить утверждение, что: $f(n) = \Omega(n^{\log_2 {4 + \epsilon}})$ Но, поскольку функция kn не может быть оценена снизу, т.е. $kn \not= \Omega(n^{\log_2 {4 + \epsilon}})$ для любого ϵ > 0, то это правило не может быть применено.

Попробуем применить 2-ё правило мастер теоремы, тогда: $f(n) = \Theta(n^{\log_2 4})$ , но и в этом случае оно не работает, т.к. $kn \not= \Theta(n^2)$ .

Рассмотрим первое правило $f(n) = O(n^{\log_2⁡ {4 - \epsilon}})$ . В этом случае $kn = O(n^{2 - \epsilon})$ при 0 < ϵ ≤ 1. Тогда $T(n) = \Theta(n^{\log_b⁡ a}) = \Theta(n^2)$ .