Линейные структуры данных

Структуры данных — это способ хранения и организации данных таким образом, чтобы облегчить доступ к этим данным и модификацию этих данных. Так, список позволяет хранить данные так, что в любой момент можно сказать, какой элемент находится перед или после. Важно отметить, что нас до какого-то момента не интересует, как конкретно реализована структура данных, а важны некоторые свойства и операции, которые можно выполнять с этой структурой.

В этом случае мы говорим про абстрактный тип данных.

К примеру, нам может быть важно иметь некоторый тип данных, который характеризуется тем, что он хранит только целые числа, а также имеет операции объединения, пересечения и разности. Используя такой тип данных, без конкретной реализации, можно придумывать алгоритмы, решающие более сложные задачи. Например, выписать простые числа используя решето Эратосфена:

1. Взять множество всех чисел, значение которых < 2 и вычесть его из множества всех целых чисел.
2. Взять наименьшее число (сейчас это будет 2) и выписать его в ответ.
3. Построить множество всех чисел, которые делятся на это число и вычесть его из текущего множества (в него попадёт и само число, т. к. оно делится само на себя).
4. Повторять шаги 2 и 3.

После чего до некоторого числа будут выписаны простые числа.

Теперь перейдём к понятию списка. Список — это абстрактный тип данных, который представляет из себя конечное число упорядоченных элементов. Каждый элемент может встречаться несколько раз, но на разных позициях. Базовой операцией, определённой на списке, является получение элемента по его индексу в списке. Если список изменяемый, то к ним добавляются операции добавления элемента в список и удаления.

Вот некоторые операции, которые можно определить для изменяемого списка:

• Создание пустого списка
• Проверка, пуст ли список или нет
• Добавление элемента в начало списка
• Добавление элемента в конец списка
• Операция получения первого элемента списка
• Операция получения элемента по заданному индексу
• Удаление элемента по заданному индексу
• и др.

На базе этих операций можно создавать и другие операции, например, чтобы поменять два элемента местами на i и i + 1 позициях достаточно удалить элемент с позиции i, и добавить его на позицию i + 1. Таким образом, элементы поменяются местами.

На языке Python абстрактный список может быть представлен в следующем виде:

class List:
    def size(self) -> int: pass
    def add(self, element: str, index: int): pass
    def remove(self, index: int): pass
    def get(self, index) -> str: pass

Здесь не реализованы, а только объявлены 4 функции: size, add, remove и get. Список в этой реализации умеет хранить и работать со строками. Также, мы явно не проверяем, что индекс для метода get, вообще говоря, подходит, т. к. список может состоять из 2-х элементов, тогда как запросить можно и элемент на позиции 30. Это приводит к неопределённости, которая обычно решается тем, что в этом случае возникает исключительная ситуация, приводящая к ошибке в программе. Избежать этих проблем можно путём проверки количества доступных элементов через метод size.

Реализуем этот абстрактный список используя структуру данных под названием связный список. Связный список состоит из указателя на первый элемент списка, который называется головой. Этот элемент содержит 2 объекта: непосредственно хранимые данные, и указатель на следующий элемент списка. Этот указатель позволяет всегда однозначно определить очередность элементов внутри. Важным следствием такой организации хранения данных является то, что доступ к данным для произвольного индекса является последовательным, т. е. чтобы получить элемент на i-м месте необходимо будет пройтись i – 1 элементу до него.

При реализации этого списка на питоне укажем, что он является реализации списка. На питоне это можно сделать, указав супер класс при определении нового класса: LinkedList(List). В секции init создадим поле, которое будет хранить ссылку на первый элемент списка. Сейчас он будет None. Также напишем вспомогательный метод, который позволит получать элемент с данными и ссылкой по его индексу в списке. Реализация такого метода несложная и состоит из итерации по указателям, начиная с головы списка, и параллельном уменьшении номер индекса. Когда индекс станет равен 0 цикл можно закончить. Отметим, что как говорилось ранее, индекс с большим значением, чем число самих элементов в списке, приведёт к ошибке, т.к. невозможно будет получить поле next у значение None.

class LinkedList(List):

    def __init__(self):
        self.head = None

    def find(self, index) -> Data:
        current = self.head
        while index > 0:
            index -= 1
            current = current.next
        return current

Реализация метода size похожа, но здесь счётчик будет использоваться для хранения результата, тогда как получение значения None по ссылке будет означать, что список закончился. Когда список размером 0, то цикл while не выполнится ни разу.

def size(self) -> int:
    count = 0
    current = self.head
    while current is not None:
        count += 1
        current = current.next
    return count

Заранее отметим, что этот метод можно улучшить, храня размер списка в отдельном поле класса size. Значения этого поля будет увеличиваться и уменьшаться в соответствующих методах вставки и удаления.

Операцию вставки нового элемента в связном списке можно выполнить так:

1. Создаём новый элемент в котором будем хранить данные.

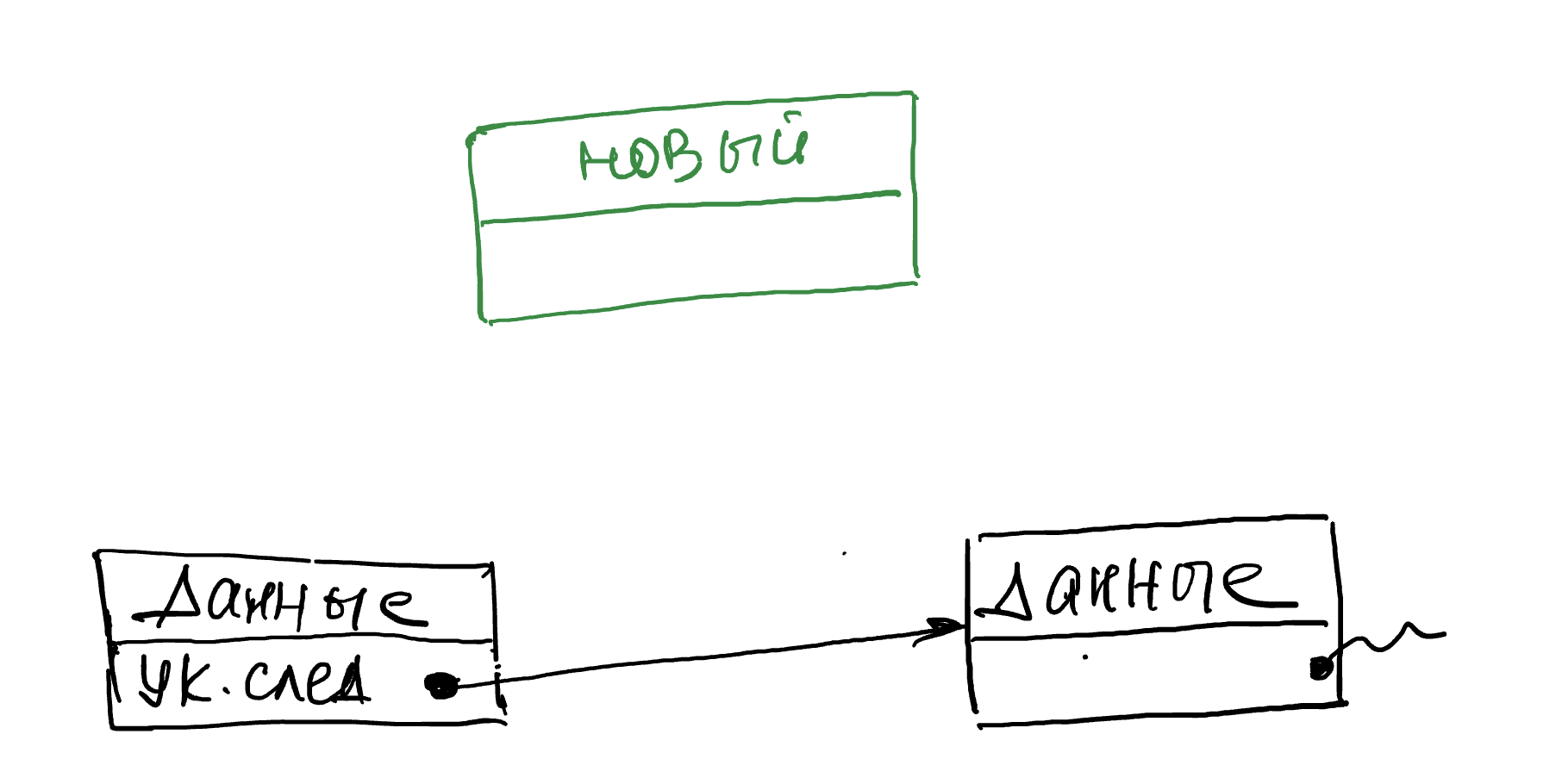
2. В новый элемент записываем ссылку, взятую из элемента, после которого будет добавлен новый элемент.

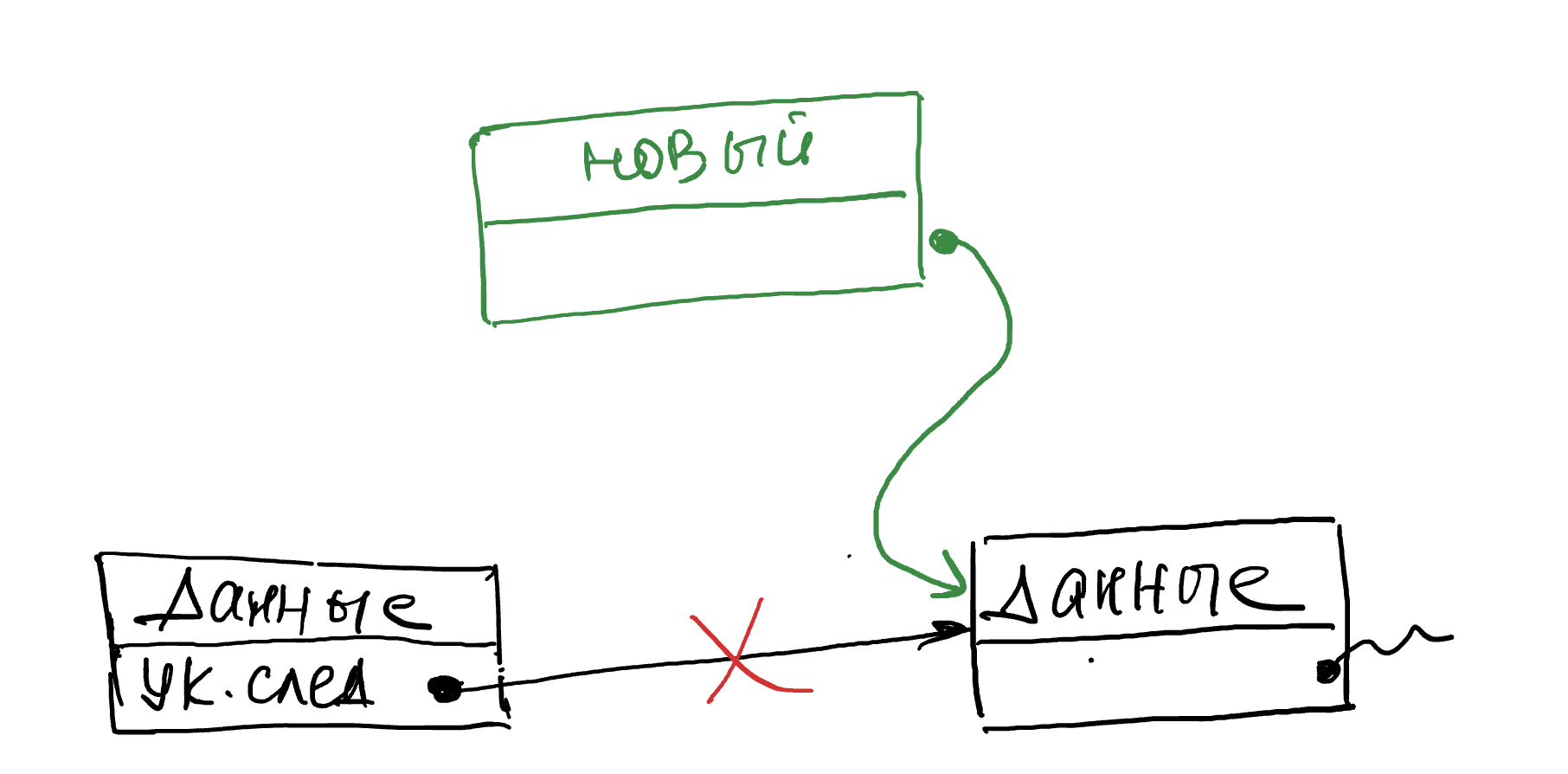
3. Записываем ссылку на новый элемент у элемента, после которого он должен оказаться.

В коде это можно выполнить так:

def add(self, element: str, index: int):
    data = Data()
    data.value = element
    if index == 0:
        data.next = self.head
        self.head = data
    else:
        prev = self.find(index - 1)
        data.next = prev.next
        prev.next = data

Обратим внимание, что после создания элемента, который здесь записан как Data() и заполнения этого элемента данными, идёт проверка, что индекс равен 0. Это необходимо, т.к. у первого элемента нет предшественника. Вместо этого, на него будет ссылаться не предшественник, а сам список.

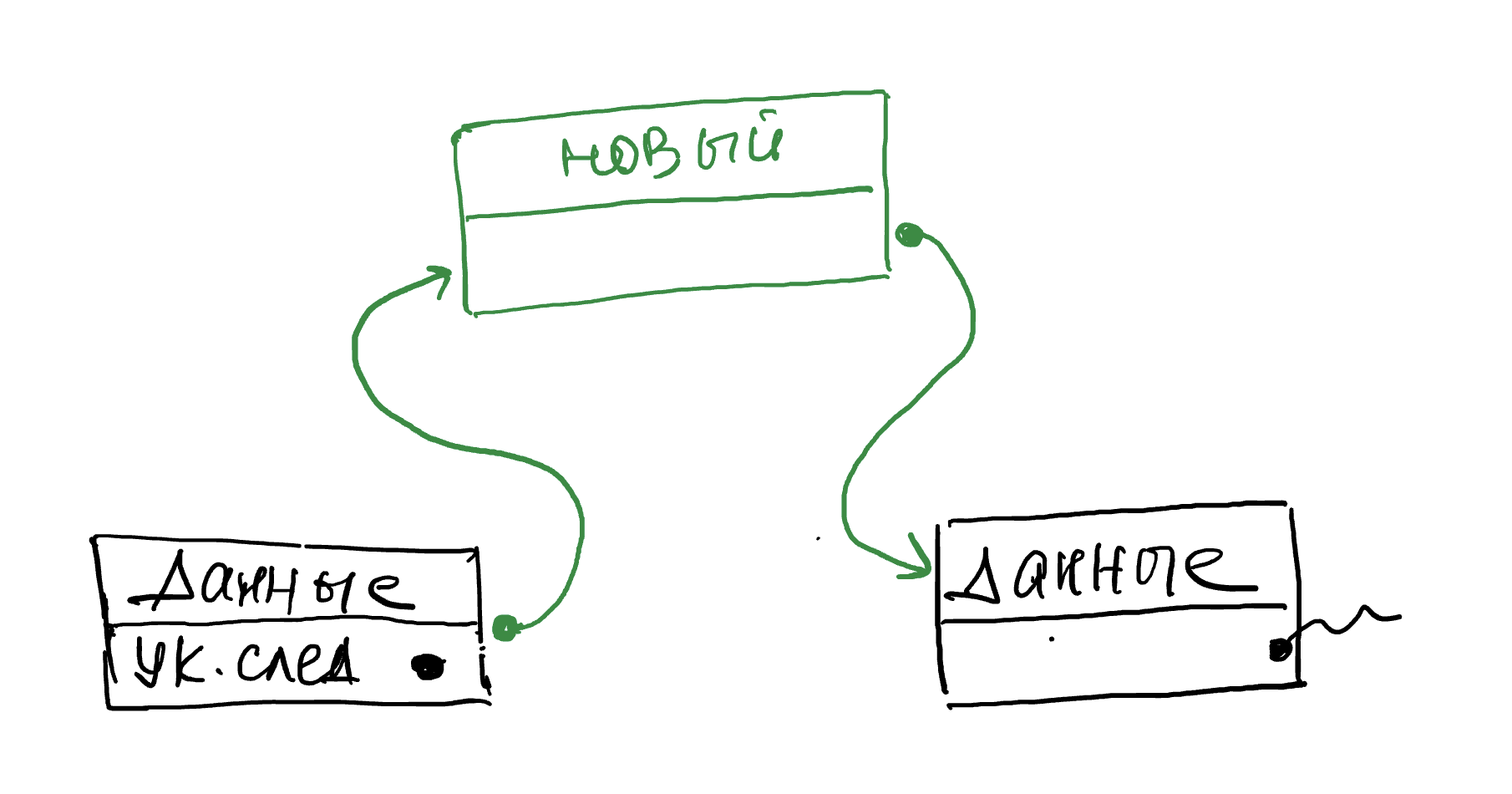
Если же элемент не первый, то работать будем с элементом на i –1 позиции. Достаточно перезаписать у этих двух элементов их ссылки: сначала записываем ссылку в новый элемент и только после этого переписываем ссылку у предшественника.

При удалении элемента из списка нам необходимо также найти предшествующий элемент, у которого нужно будет обновить ссылку.

Как только ссылка будет скопирована, то удаляемый элемент можно просто удалить.

Реализация на питоне достаточно простая и так же отдельно учитывает обработку первого элемента, при удалении которого необходимо обновлять не предшественника, а поменять ссылку на первый элемент у самого списка.

def remove(self, index: int):
    if index == 0:
        self.head = self.head.next
    else:
        prev = self.find(index - 1)
        prev.next = prev.next.next

Теперь рассмотрим другую реализацию списка, которая может иметь названия «динамический массив», «вектор» или «список на массивах». На рисунке роль списка играет пунктирная линия, которая включает в себя обычный массив. Здесь массив — это неизменяемая структура данных, размер которой фиксирован и не может быть изменён. В памяти компьютера под такие массивы необходимое количество места выделяется сразу, поэтому впоследствии их нельзя расширить. Главным преимуществом массива является то, что доступ к произвольному элементу выполняется за константное время.

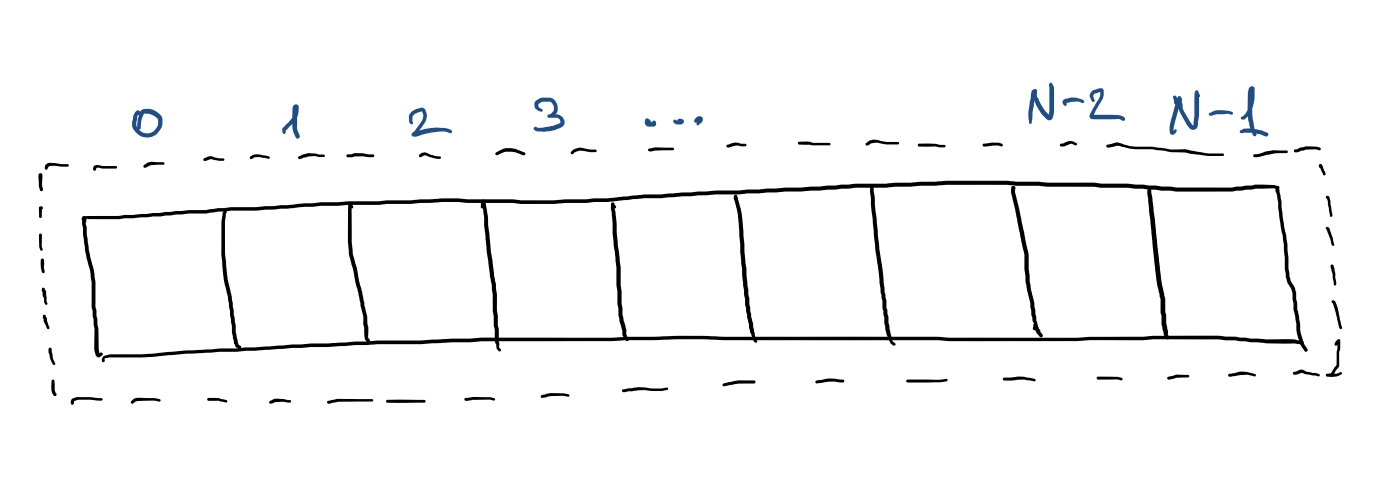
На питоне создание нового массива можно реализовать примерно таким образом.

def allocate_array(size: int) -> list:
    return [None] * size

Важно отметить, что размер массива ≠ размеру списка. Массив используется для хранения элементов, но элементы в нём могут занимать не все ячейки. Когда место под новые элементы есть, то мы можем добавлять их в конец.

Проблема возникает, когда ячейки закончились, а новый элемент добавить нужно.

В этом случае создают новый массив большего размера. Например, можно увеличить его на 1 элемент или сразу в 2 раза, как в этом примере.

После чего все элементы из первого копируются во второй, и дальше добавляется новый элемент.

В конце старый массив просто удаляется.

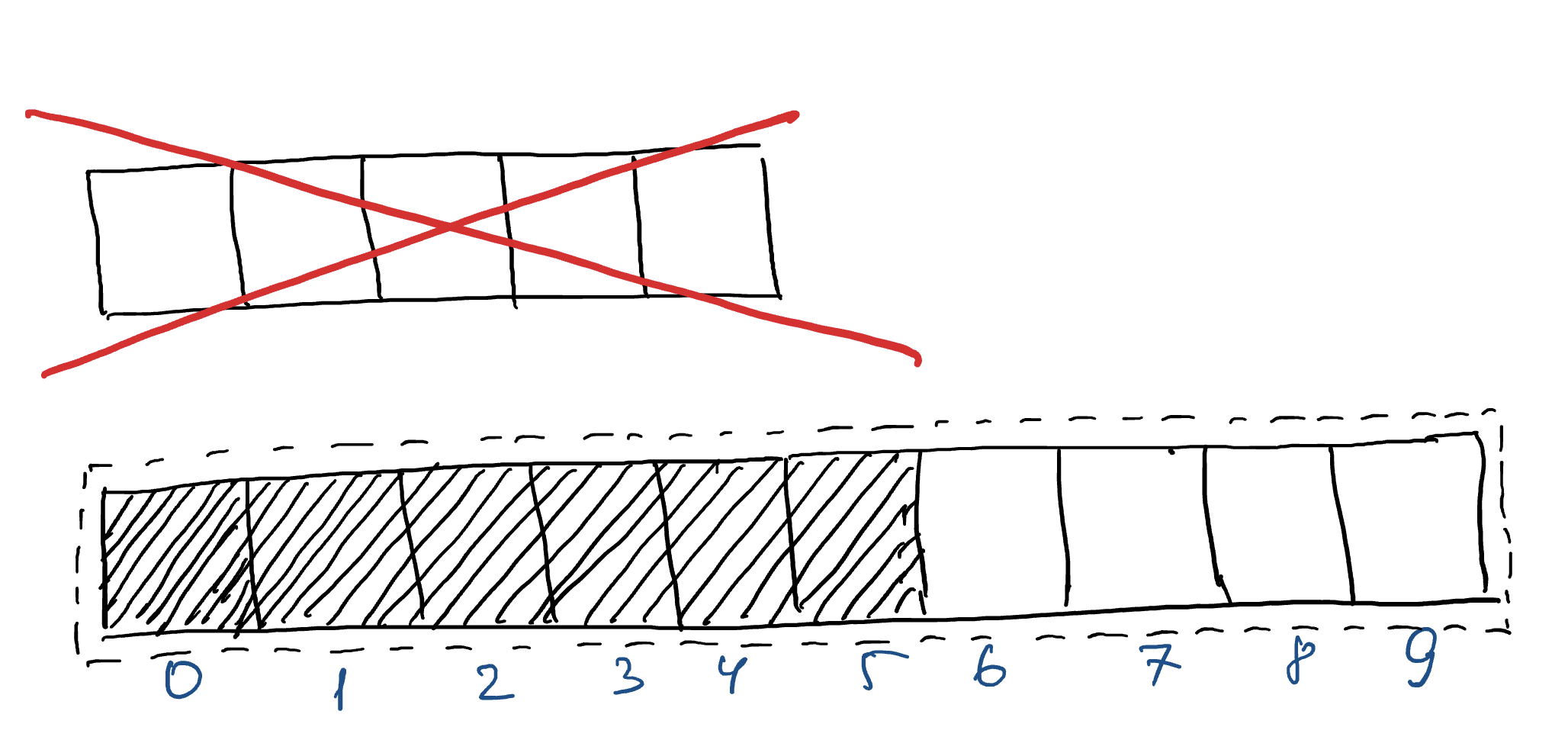
Напишем на питоне такую процедуру, которая будет называться ensure_capacity, в которой и реализуем процедуру создания нового массива и копирования в него данных. Эта процедура позволит быстро создать массив нужного размера при добавлении нового элемента.

def allocate_array(size: int) -> list:
    return [None] * size


def ensure_capacity(self, size: int):
    if self._size < size:
        new_array = allocate_array(len(self.array) * 2)
        self.copy(self.array, new_array)
        self.array = new_array

Рассмотрим также случай, когда новый элемент добавляется не в конец списка, а где-то между.

Тогда, чтобы записать элемент на нужное место необходимо сдвинуть все элементы дальше на 1.

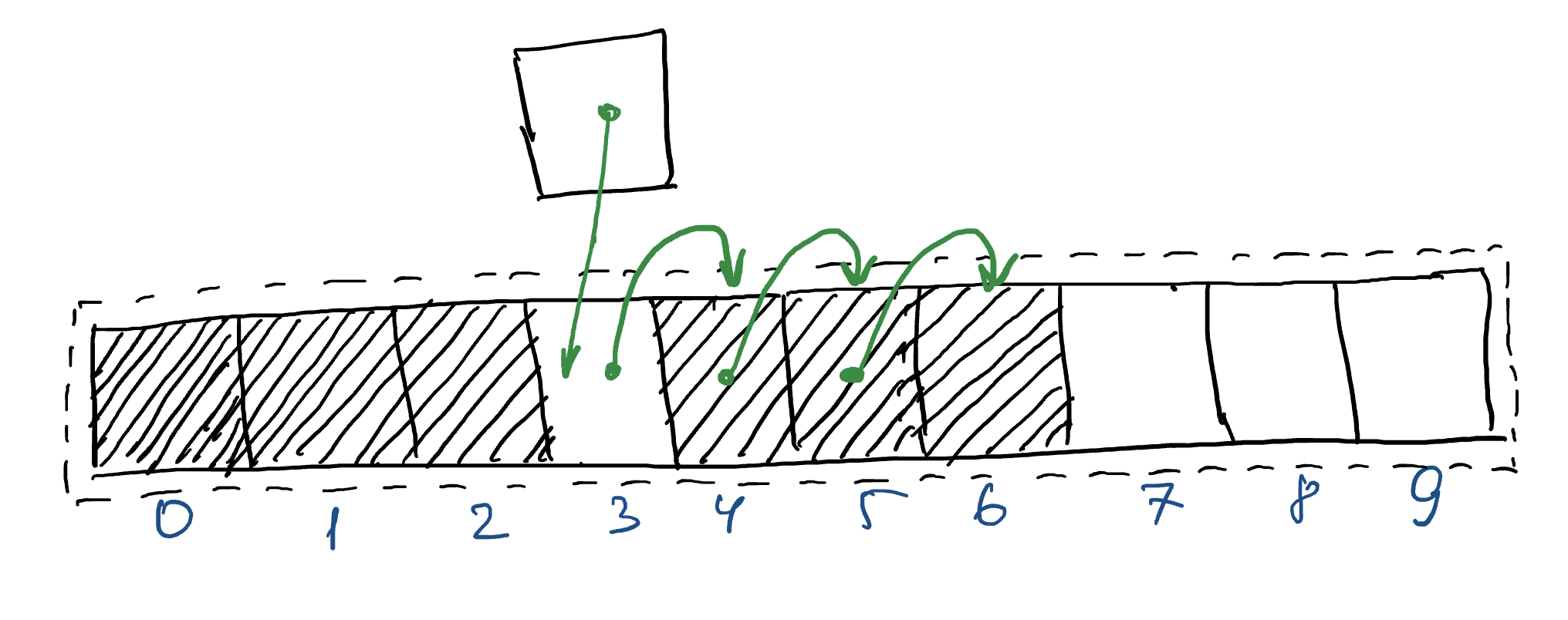
В реализации на питоне такое копирование можно начать с конца списка. Необходимо не забыть также увеличить размер самого списка на 1.

def add(self, element: str, index: int):
    if index > self._size + 1:
        raise ValueError
    self.ensure_capacity(self._size + 1)
    for i in reversed(range(index + 1, self._size + 1)):
        self.array[i] = self.array[i - 1]
        self.array[index] = element
    self._size += 1

Аналогичные рассуждения применимы при удалении элемента из списка. Обратим внимание, что при удалении массива можно выполнять операцию, обратную операции по созданию массива большего размера. Но на практике это делают редко.

Мы рассмотрели 2 реализации для абстрактного списка. Каждая из них имеет свои временные оценки сложности для основных операций. Связный список требует линейное время почти всегда. Исключение — работа с началом списка, где все операции будут занимать константное время. Для динамического массива операция по получению элемента — константное. Но при добавлении элементов в начало или удалении из начала из-за копирования сложность линейная.

Существуют и другие линейные структуры, такие как очередь. Для очереди определены 2 операции: вставка элемента в очередь и удаление элемента из очереди. При этом, если какой-то элемент был добавлен раньше другого элемента, то именно он первым будет удалён из списка. Такая организация называется «Первый вошёл, первый вышел». Аббревиатура FIFO расшифровывается именно так: First in, first out.

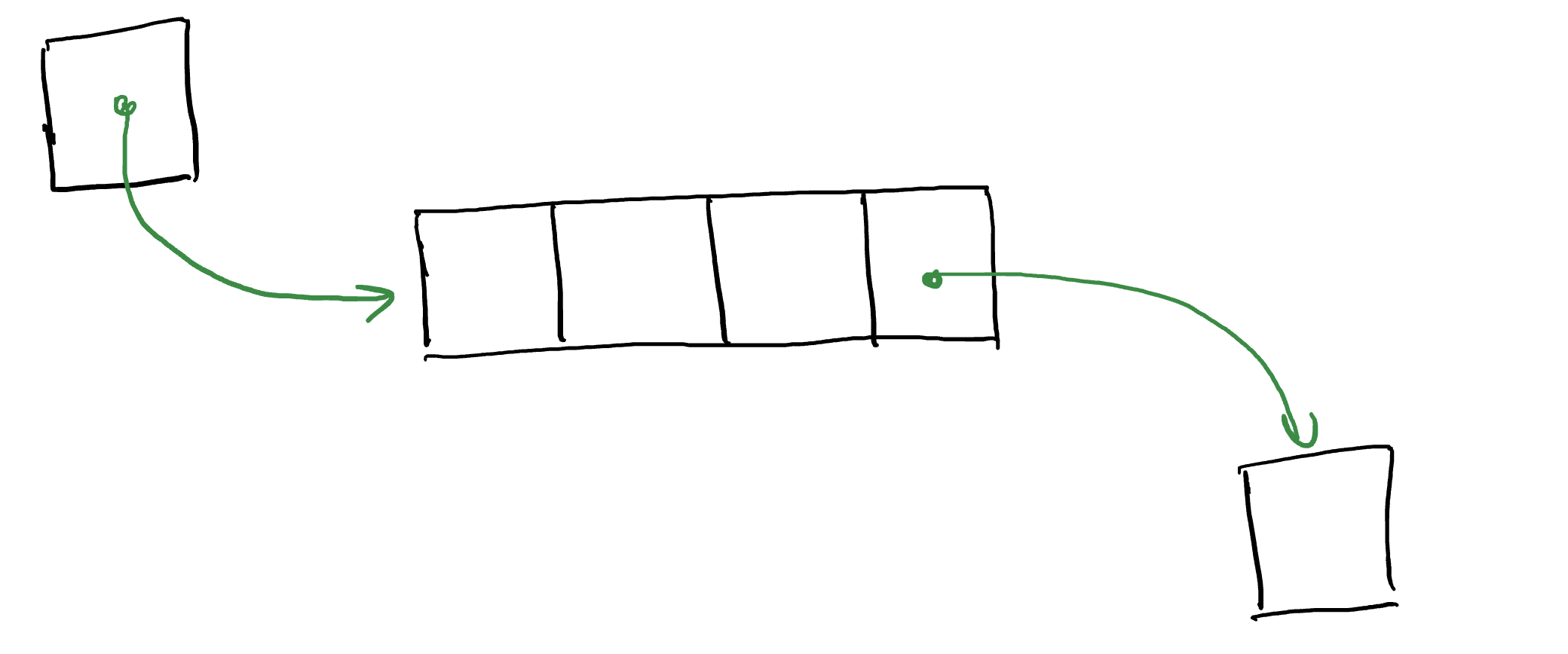
Очередь можно реализовать, используя список. Тогда операция добавления в очередь будет тем же самым, что и добавление элемента в конец списка. Операция удаления будем иметь смысл удаления из начала списка.

def enqueue(self, element: str):
    self._list.append(element)

def dequeue(self) -> str:
    value = self._list.get(0)
    self._list.remove(0)
    return value

Ещё одна важная структура данных — это стек. Он организован по принципу «первый вошёл, последний вышел». Эта структура много, где используется, например, для хранения истории изменений в текстовом редакторе, когда пользователь нажимает «отменить». Каждое изменение записывается в стек, а когда он хочется удалить последние несколько изменений, то они извлекаются из стека.

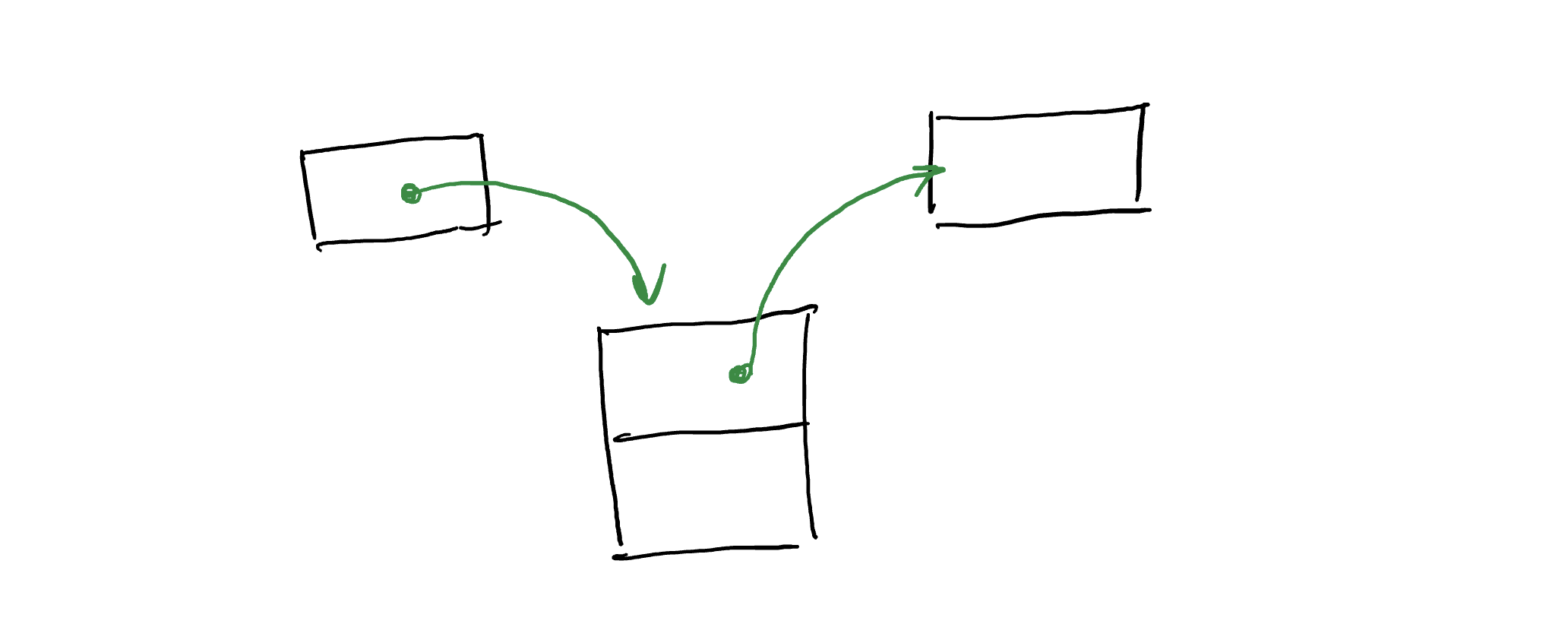
Реализуем стек с использованием списка. Определим операции push и pop, которые соответственно добавляют элемент в начало очереди и удаляют элемент из начала очереди.

def push(self, element: str):
    self._list.append(0)

def pop(self) -> str:
    value = self._list.get(0)
    self._list.remove(0)
    return value

При такой организации оказывается, что использование динамического массива является крайне невыгодным, т.к. в нём добавление в начало списка будет означать копирование всех элементов дальше на 1. Ровно то же самое копирование будет происходить и при удалении элемента из начала списка. Если же использовать связный список, то обе эти операции будут всегда приводить лишь к изменению ссылки на первый элемент списка, что означает работу за константное время. Таким образом, выбор реализации довольно сильно влияет на время работы самого стека.